Schoenflies problem

In mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies.

Original formulation

It states that not only does every simple closed curve in the plane separate the plane into two regions, one (the "inside") bounded and the other (the "outside") unbounded; but also that these two regions are homeomorphic to the inside and outside of a standard circle in the plane.

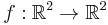An alternative statement is that if C \subset \mathbb R^2 is a simple closed curve, then there is a homeomorphism f�: \mathbb R^2 \to \mathbb R^2 such that 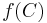f(C) is the unit circle in the plane.

Such a theorem is only valid in two dimensions. In three dimensions there are counterexamples such as Alexander's horned sphere. Although they separate space into two regions, those regions are so twisted and knotted that they are not homeomorphic to the inside and outside of a normal sphere.

Generalizations

There does exist a higher-dimensional generalization due to Morton Brown and independently Barry Mazur with Marston Morse, which is also called the generalized Schoenflies theorem. It states that, if an (n − 1)-dimensional sphere S is embedded into the n-dimensional sphere Sn in a locally flat way (that is, the embedding extends to that of a thickened sphere), then the pair (Sn, S) is homeomorphic to the pair (Sn, Sn−1), where Sn−1 is the equator of the n-sphere. Brown and Mazur received the Veblen Prize for their contributions.

The Schoenflies problem can be posed in categories other than the topologically locally flat category, i.e. does a smoothly (piecewise-linearly) embedded (n − 1)-sphere in the n-sphere bound a smooth (piecewise-linear) n-ball? For n = 4, the problem is still open for both categories. See Mazur manifold. For n ≥ 5 the question has an affirmative answer, and follows from the h-cobordism theorem.

References